A sinus- és koszinusztétel alapjai és jelentősége
A háromszögek tanulmányozása a matematika egyik legizgalmasabb és legpraktikusabb területe, amely mind a középiskolai, mind az egyetemi tanulmányok során előkerül. A különböző háromszögek tulajdonságainak megértése nemcsak az elméleti tudás szempontjából fontos, hanem számos mérnöki, építészeti és mindennapi probléma megoldásában is kulcsszerepet játszik. A háromszögek oldallal és szögekkel kapcsolatos összefüggései közül kiemelkedő jelentőségű a sinus- és koszinusztétel, amelyek segítségével ismeretlen oldalakat vagy szögeket számíthatunk ki. Ez az írás azért készült, hogy mind a kezdők, mind a haladók számára átfogó és gyakorlati útmutatót nyújtson a sinus- és koszinusztétel témakörében.
Az olvasó részletesen megismerheti a tételek matematikai alapjait, alkalmazási területeit, gyakorlati példákat, valamint a leggyakoribb hibákat és azok elkerülésének módját. Először is, tisztázzuk, hogy mi is az a sinus- és koszinusztétel, miért nevezzük őket a háromszögek „kulcsainak”, és hogyan teszik lehetővé a háromszög oldalainak és szögeinek kiszámítását. A cikk nem csupán a képleteket mutatja meg, hanem konkrét, lépésenkénti példákon keresztül segíti azok megértését. Továbbá szó lesz a mindennapos és speciális felhasználási területekről, legyen szó földmérésről, fizikáról, vagy akár egyszerű hobbitevékenységekről.
A matematika világában a háromszögek mindenütt jelen vannak, és a sinus- valamint koszinusztétel a leghatékonyabb eszközök közé tartoznak a háromszögek problémáinak megoldásában. Ezek a tételek nem korlátozódnak csak derékszögű háromszögekre, hanem bármilyen típusú háromszög esetén alkalmazhatók, ami jelentősen bővíti a lehetőségeket. A cikk célja, hogy a sinus- és koszinusztétel alkalmazásával magabiztosan és pontosan tudjunk számolni, elkerülve a leggyakoribb hibákat.
A következőkben először a sinus- és koszinusztétel matematikai levezetésével és jelentőségével foglalkozunk, majd rátérünk azok gyakorlati alkalmazására. Külön fejezetben tárgyaljuk a legjellemzőbb hibákat, valamint hasznos tanácsokat adunk a sikeres feladatmegoldáshoz. Végül egy átfogó GYIK (FAQ) segít összefoglalni a legfontosabb tudnivalókat és eloszlatja a gyakori félreértéseket.
A sinus-tétel alkalmazása háromszögekben
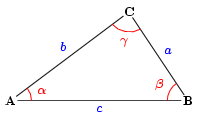
A sinus-tétel (más néven szinusz-tétel) az egyik legalapvetőbb eszköz a háromszögek számítása során, különösen akkor, ha nem derékszögű háromszöggel dolgozunk. A tétel kimondja, hogy bármely háromszögben az oldalak hosszának aránya a szemközti szögek szinuszához megegyezik. Ez a következő képlettel fejezhető ki:
a / sin(α) = b / sin(β) = c / sin(γ)
Itt „a”, „b” és „c” a háromszög oldalainak hossza, míg „α”, „β” és „γ” a velük szemközti szögek. Ez az összefüggés lehetővé teszi, hogy ha például két oldal hosszát és egy szöget ismerünk, akkor a harmadik oldalt vagy egy ismeretlen szöget is könnyedén kiszámíthatunk. A sinus-tétel fő előnye, hogy általános érvényű, tehát bármilyen háromszögre igaz, legyen az hegyesszögű, tompaszögű vagy akár szabályos háromszög.
Vegyünk egy konkrét példát: Tegyük fel, hogy van egy háromszögünk, ahol az „a” oldal hossza 8 cm, a „b” oldal hossza 5 cm, és az α szög 30°. Szeretnénk kiszámítani a β szöget. A sinus-tétel alapján írhatjuk:
8 / sin(30°) = 5 / sin(β)
Mivel sin(30°) = 0,5, ezért:
8 / 0,5 = 5 / sin(β)
16 = 5 / sin(β)
Innen:
sin(β) = 5 / 16
sin(β) ≈ 0,3125
β ≈ arcsin(0,3125) ≈ 18,2°
Ez a példa jól mutatja, hogy a sinus-tétel segítségével könnyen ki tudunk számolni ismeretlen szöget vagy oldalt, amennyiben a szükséges adataink megvannak. A sinus-tétel különösen akkor hasznos, amikor két szöget és egy oldalt (SAS vagy SSA eset) ismerünk egy háromszögben.
Mikor alkalmazzuk a sinus-tételt?
A sinus-tétel alkalmazásának leggyakoribb esetei közé tartoznak az ASA, AAS és SSA esetek. Ezek jelentése:
- ASA (Angle-Side-Angle): Két szöget és a közrezárt oldalt ismerünk.
- AAS (Angle-Angle-Side): Két szöget és egy, az egyikhez tartozó oldalt ismerünk.
- SSA (Side-Side-Angle): Két oldalt és az egyik hozzájuk tartozó szöget ismerünk.
A következő táblázat segít áttekinteni, mikor érdemes a sinus-tételt használni:
| Ismert adatok | Ajánlott tétel |
|---|---|
| 2 szög + 1 oldal (ASA/AAS) | Sinus-tétel |
| 2 oldal + 1 szemközti szög (SSA) | Sinus-tétel (de két lehetséges háromszög is lehet!) |
| 2 oldal + közrezárt szög (SAS) | Koszinusztétel |
| 3 oldal (SSS) | Koszinusztétel |
Fontos megjegyezni, hogy az SSA esetben néha két különböző háromszög is kialakulhat ugyanazzal az adathalmazzal (kettős értelmű eset). Ilyenkor külön oda kell figyelni a számítás során, hogy melyik lehetséges eredményt vesszük figyelembe.
Koszinusztétel: a kiterjesztett Pitagorasz-tétel
A koszinusztétel (vagy cosinus-tétel) szintén alapvető szerepet játszik a háromszögoldalak és -szögek számításában, főleg akkor, amikor a sinus-tétel már nem alkalmazható közvetlenül. A koszinusztételt gyakran a Pitagorasz-tétel általánosításaként is emlegetik, hiszen ha a háromszög derékszögű, a képlet egyszerűen a Pitagorasz-tételre egyszerűsödik.
A koszinusztétel képlete a következő:
c² = a² + b² – 2ab*cos(γ)
Hasonlóan, a másik két oldalra is alkalmazható:
a² = b² + c² – 2bccos(α)
b² = a² + c² – 2accos(β)
Ez a tétel különösen hasznos, amikor két oldal és a közbezárt szög (SAS), vagy három oldal (SSS) ismeretében kell számolnunk. Például, ha két oldal hosszát és a közrezárt szöget ismerjük, akkor a harmadik oldal hosszát tudjuk kiszámítani. Ugyanakkor, ha mindhárom oldalt ismerjük, akkor bármelyik szöget meghatározhatjuk.
Lássunk egy példát: Adott egy háromszög, ahol a = 6 cm, b = 8 cm és a közbezárt szög γ = 60°. Mekkora a harmadik oldal, c?
c² = 6² + 8² – 268cos(60°)
c² = 36 + 64 – 2680,5
c² = 100 – 48
c² = 52
c = √52 ≈ 7,21 cm
Így a harmadik oldal hossza kb. 7,21 cm lesz.
A koszinusztétel további felhasználásai
A koszinusztétel nagy előnye, hogy a háromszög minden oldalára és szögére egyaránt alkalmazható, és nem szükséges, hogy derékszögű legyen a háromszög. Ha mindhárom oldal ismert, akkor bármelyik szöget meghatározhatjuk, például:
cos(γ) = (a² + b² – c²) / (2ab)
Ez a képlet lehetővé teszi, hogy három oldal hosszából kiszámítsuk a háromszög bármelyik szögét – ezt nevezik a háromszög szögeinek „inverz” meghatározásának.
A koszinusztétel további előnye, hogy „átmenetet” biztosít a derékszögű és általános háromszögek között. Amikor a háromszög derékszögű, γ = 90°, így cos(90°) = 0, és a képlet:
c² = a² + b²
Ez éppen a jól ismert Pitagorasz-tétel. Tehát a koszinusztételt akár úgy is felfoghatjuk, mint a Pitagorasz-tétel általánosított, minden háromszögre igaz verzióját.
Sinus- és koszinusztétel összehasonlítása: Mikor melyiket használjuk?
| Helyzet | Sinus-tétel | Koszinusztétel |
|---|---|---|
| 2 szög + 1 oldal | Igen | Nem ajánlott |
| 2 oldal + közrezárt szög | Nem ajánlott | Igen |
| 3 oldal | Nem ajánlott | Igen |
| 2 oldal + egy szög (nem közrezárt) | Igen (de kettős megoldás lehet) | Nem ajánlott |
| Derékszögű háromszög | Igen (egyszerűbb a trigonometria) | Igen (egyszerűsödik a Pitagorasz-tételre) |
Gyakorlati példák a tétel felhasználására
A sinus- és koszinusztétel nem csupán elméleti jelentőségű, hanem a mindennapokban és számos szakterületen is hasznos eszköz. Gondoljunk például a földmérésre, ahol gyakran nem lehet közvetlenül megmérni egy terület oldalait vagy szögeit. Ilyenkor a háromszögek és a hozzájuk kapcsolódó tételek, különösen a sinus- és koszinusztétel alkalmazása jelent megoldást.
Képzeljünk el egy példát: Egy öböl két partján állunk, és szeretnénk meghatározni a két pont távolságát (amit közvetlenül nem tudunk megmérni, mert víz választ el). A két parton felállítunk két mérési pontot (A és B), az öböl két oldalán, és egy harmadik pontot (C) ismerünk a part egyik oldalán. A három pont háromszöget alkot, ahol két oldal (AC és BC) hossza és a bezárt szög ismert. A koszinusztétel segítségével meghatározható a két part közötti távolság.
Legyen például:
- AC = 120 m
- BC = 200 m
- A bezárt szög (∠C) = 45°
Az AB oldal a keresett érték, amit a koszinusztétellel számolunk:
AB² = AC² + BC² – 2ACBC*cos(45°)
AB² = 120² + 200² – 2120200*0,7071
AB² = 14 400 + 40 000 – 33 710
AB² = 54 400 – 33 710
AB² = 20 690
AB ≈ √20 690 ≈ 144 m
Tehát a két part közötti távolság kb. 144 méter. Ez a módszer jól mutatja, hogy a koszinusztétellel a gyakorlatban is gyorsan és pontosan tudunk számolni.
Háromszög oldalának meghatározása szögméréssel – sinus-tétel a gyakorlatban
A sinus-tétel különösen hasznos, amikor például egy háromszög két szögét és egy oldalát ismerjük, és szeretnénk meghatározni a többi oldalt. Képzeljük el, hogy egy háromszögben az egyik oldal hossza 10 cm, az ehhez tartozó szög α = 30°, a másik szög β = 80°. Mekkora a „b” oldal hossza?
Első lépésként meghatározzuk a harmadik szöget:
γ = 180° – (30° + 80°) = 70°
A sinus-tétel alapján:
a / sin(α) = b / sin(β)
10 / sin(30°) = b / sin(80°)
Mivel sin(30°) = 0,5 és sin(80°) ≈ 0,9848:
10 / 0,5 = b / 0,9848
20 = b / 0,9848
b = 20 * 0,9848 ≈ 19,696 cm
Tehát a „b” oldal kb. 19,7 cm hosszú.
Összefoglalva, a sinus- és koszinusztétel nem csupán tankönyvi érdekesség, hanem a gyakorlati számítások, mérések és tervezések nélkülözhetetlen eszköze.
Tipikus hibák és tanácsok a tételek használatához
Még a tapasztaltabb tanulóknál is előfordulhatnak hibák a sinus- és koszinusztétel alkalmazása során. Az egyik leggyakoribb hiba a szög mértékegységének tévesztése: a számológépek sokszor alapból radiánban dolgoznak, miközben a feladat fokban adja meg a szögeket. Ha például a szög 60°, de a számológép radián üzemmódban van, teljesen hibás eredmény jöhet ki.
Egy másik gyakori hiba az, amikor az SSA-esetben (két oldal és az egyikhez tartozó szög ismert) a tanulók nem gondolnak arra, hogy két különböző háromszög is létezhet (az ún. kettős értelmű eset). Például ha az egyik szög 30°, és a hozzá tartozó oldal rövid, előfordulhat, hogy ugyanezekkel a paraméterekkel egy másik háromszög is felrajzolható, más szögekkel. Ilyenkor mindkét lehetőséget végig kell gondolni.
További tipikus hiba, hogy a koszinusztétel alkalmazásakor a képletbe rosszul helyettesítik be a szögeket vagy oldalakat, illetve elfelejtik a négyzetgyökvonást az oldal meghatározásánál. Szintén fontos figyelni a zárójelekre – különösen, ha kézzel számolunk vagy számológépet használunk –, mert egy zárójelhiba a számítás végét jelentheti.
Hasznos tanácsok a sikeres feladatmegoldáshoz
- Mindig ellenőrizd a szög mértékegységét! Ellenőrizd, hogy a számológép fok vagy radián üzemmódban van-e.
- Rendszerezetten dolgozz: Írd fel a háromszög oldalait és szögeit világosan, mielőtt a képletbe helyettesítenél.
- Ellenőrizd az eredményt: Ellenőrizd, hogy a kiszámolt szög vagy oldal reálisan illeszkedik-e a háromszöghöz.
- Az SSA-esetben vizsgáld meg a kettős lehetőséget: Lehetséges, hogy két különböző háromszög is kialakulhat.
- Használj táblázatot: Ha sok adatod van, egy táblázat segít átlátni az összefüggéseket.
- Gyakorolj sokat: Minél többet gyakorolsz, annál rutinosabban és gyorsabban megy majd a feladatmegoldás.
- Ne feledkezz meg a háromszög szögösszegéről: A háromszög belső szögeinek összege mindig 180°, ezt használd az ellenőrzésre.
- Különösen figyelj a koszinusztétel négyzetgyöközésére: Ha oldalt számolsz, ne felejtsd el a végén a négyzetgyökvonást.
- Egységek egységesítése: Az oldalak és szögek egységét mindig tartsd konzisztensen!
- Tanulj a hibákból: Ha elrontasz valamit, nézd át újra lépésről lépésre a számítás menetét.
Az alábbi egyszerű táblázat összefoglalja a leggyakoribb hibákat és azok elkerülésének módját:
| Hiba típusa | Megelőzésének módja |
|---|---|
| Helytelen szög-egység | Ellenőrizd a számológép beállítását |
| Kettős értelmű SSA eset | Mindkét megoldást vizsgáld meg |
| Képletsorrend és zárójelek | Gondosan írj zárójeleket |
| Négyzetgyök elfelejtése | Ellenőrizd a képletet lépésenként |
| Oldal/szög eltévesztése | Jelöld be a háromszögön az adatokat |
GYIK – Gyakran Ismételt Kérdések 😃
1. Mi a sinus-tétel alapképlete? 🤔
a / sin(α) = b / sin(β) = c / sin(γ)
2. Mikor használjuk a koszinusztételt? 🧐
Akkor, ha két oldal és a közrezárt szög (SAS) vagy mindhárom oldal (SSS) ismert.
3. Lehet-e a sinus-tételt derékszögű háromszögben használni? 🎯
Igen, de ott egyszerűbb a szögfüggvények szokásos alkalmazása.
4. Mi az SSA-eset nehézsége? 🛑
Kettős értelmű megoldás, két háromszög is létezhet ugyanazzal az adathalmazzal.
5. Mit tegyek, ha a számológépem radiánban számol? 🔄
Állítsd át fok módba, ha a feladat szögei fokban adottak.
6. Miért nevezik a koszinusztételt a „kiterjesztett Pitagorasz-tételnek”? 🧮
Mert derékszög esetén a Pitagorasz-tételre egyszerűsödik.
7. Milyen hibákat érdemes elkerülni a képletek használatakor? ⚠️
Szög mértékegység, zárójelek, kettős SSA-eset figyelmen kívül hagyása.
8. Használhatók ezek a tételek minden háromszögre? 🔺
Igen, bármilyen (nem feltétlenül derékszögű) háromszögre alkalmazhatók.
9. Mit jelent a „közrezárt szög”? 🔄
Két ismert oldal által közrezárt, azaz közöttük lévő szög.
10. Hogyan ellenőrizzem a számításaim helyességét? ✅
Ellenőrizd a háromszög szögösszegét (180°), és hogy az oldalak hossza reális-e.
Reméljük, hogy ez a cikk segített megérteni és helyesen alkalmazni a sinus- és koszinusztételt!
Matematika kategóriák
- Matek alapfogalmak
- Kerületszámítás
- Területszámítás
- Térfogatszámítás
- Felszínszámítás
- Képletek
- Mértékegység átváltások
Még több érdekesség: